【図解】倍数比例の法則とは、「2種類の元素AとBが化合して，いくつかの異なる化合物を作るとき，一定質量のAとBの質量の間には，簡単な整数比が成り立つ。」というものです。本記事では、倍数比例の法則について具体例を踏まえてわかりやすく解説します。発見者ドルトンもセットで覚えましょう。
ちなみに僕は１０年以上にわたりプロとして個別指導で物理化学を教えてきました。
おかげさまで、個別指導で教えてきた生徒は1000名以上、東大京大国公立医学部合格実績は100名以上でして、目の前の生徒だけでなく、高校化学で困っている方の役に立てればと思い、これまでの経験をもとに化学の講義をまとめています。参考になれば幸いです。
倍数比例の法則とは
倍数比例の法則とは、「2種類の元素AとBが化合して，いくつかの異なる化合物を作るとき，一定質量のAとBの質量の間には，簡単な整数比が成り立つ。」というものです。
【例】
例えば、一酸化炭素28 gと二酸化炭素44 gは、それぞれ同量の炭素12 gを含んでいます。
（炭素の原子量C = 12 、酸素の原子量O = 16）
一酸化炭素28 g中の酸素は16 gであり、二酸化炭素44 g中の酸素は32 gとなります。
つまり、一定量の炭素を含む一酸化炭素と二酸化炭素それぞれに含まれる酸素の質量の比は、1：2 という比で表されます。これが倍数比例の法則です。
![倍数比例の法則の説明]()
炭素原子1個に対し酸素原子が1個結合した化合物が一酸化炭素であり、炭素原子1個に対し酸素原子が2個結合した化合物が二酸化炭素です。
原子はそれ以上分割できない粒子なので、炭素原子1個に対し酸素原子は必ず整数個結合するため、倍数比例の法則が成り立ちます。
倍数比例の法則の発見者ドルトン
![ドルトン]()
出典：https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%A7%E3%83%B3%E3%83%BB%E3%83%89%E3%83%AB%E3%83%88%E3%83%B3
倍数比例の法則の発見者はドルトンであり、発見した年は1803年です。
組合せが出題されるので覚えておきましょう。
以下に暗記方法を記載していますので、参考にしてください。
さいごに
倍数比例の法則の内容を説明できるようにしておくと暗記がしやすいと思いますので、復習を心がけてください。
なお、僕がこれまで1000名以上の個別指導で、生徒の成績に向き合ってきた経験をもとにまとめた化学の勉強法も参考にしてもらえれば幸いです。
また、本記事をググってくださったときのように、参考書や問題集を解いていて質問が出たときに、いつでもスマホで質問対応してくれる塾はこれまでありませんでした。
しかし、2020年より駿台がこの課題を解決してくれるサービスmanaboを開始しました。今のところ塾業界ではいつでも質問対応できるのは駿台だけかと思います。塾や予備校を検討している方の参考になれば幸いです。
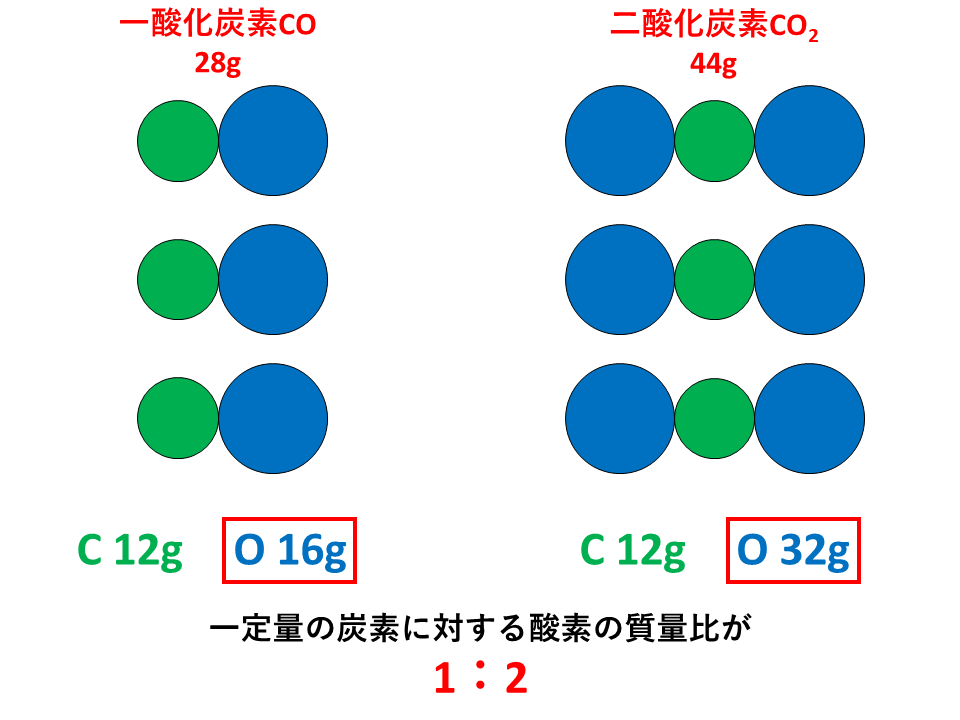炭素原子1個に対し酸素原子が1個結合した化合物が一酸化炭素であり、炭素原子1個に対し酸素原子が2個結合した化合物が二酸化炭素です。
原子はそれ以上分割できない粒子なので、炭素原子1個に対し酸素原子は必ず整数個結合するため、倍数比例の法則が成り立ちます。
出典：https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%A7%E3%83%B3%E3%83%BB%E3%83%89%E3%83%AB%E3%83%88%E3%83%B3
倍数比例の法則の発見者はドルトンであり、発見した年は1803年です。
組合せが出題されるので覚えておきましょう。
以下に暗記方法を記載していますので、参考にしてください。
